Analytical Foundations of ECE #

Complex Numbers #

Definition of a Complex Number #

Consider \(x^2-1=0\) . To find the roots: \[\begin{aligned} x^2-1 &= 0\\ x^2 &= 1\\ x &= \sqrt{1}\\ \rArr x &= \plusmn{1} \end{aligned}\]

Now consider \(x^2+1=0\) : \[\begin{aligned} x^2 + 1 &= 0\\ x^2 &= -1\\ x &= \sqrt{-1}\\ \rArr x &= \plusmn{j} \end{aligned}\]

\(j\) is an imaginary unit introduced to solve this type of equation. It is better known as \(i\) : \[i^2 = -1 \begin{cases} \text{Mathematics} \\ \text{Physics} \\ \text{Chemistry} \end{cases}\\\] \[ j^2 = -1 \begin{cases} \text{Engineering} \end{cases}\]

A complex number is represented as \(z = a+jb\) , where: \[\begin{aligned} a &= Re(z)\ &\text{Real part of z}\\ b &= Im(z)\ &\text{Imaginary part of z} \end{aligned}\]

Complex Number Example #

Sketch the following complex numbers in the 2D complex plane.

• \(z_1 = 1 + j2\)

• \(z_2 = -1 + j2\)

• \(z_3 = -1 - j2\)

• \(z_4 = 1 - j2\)

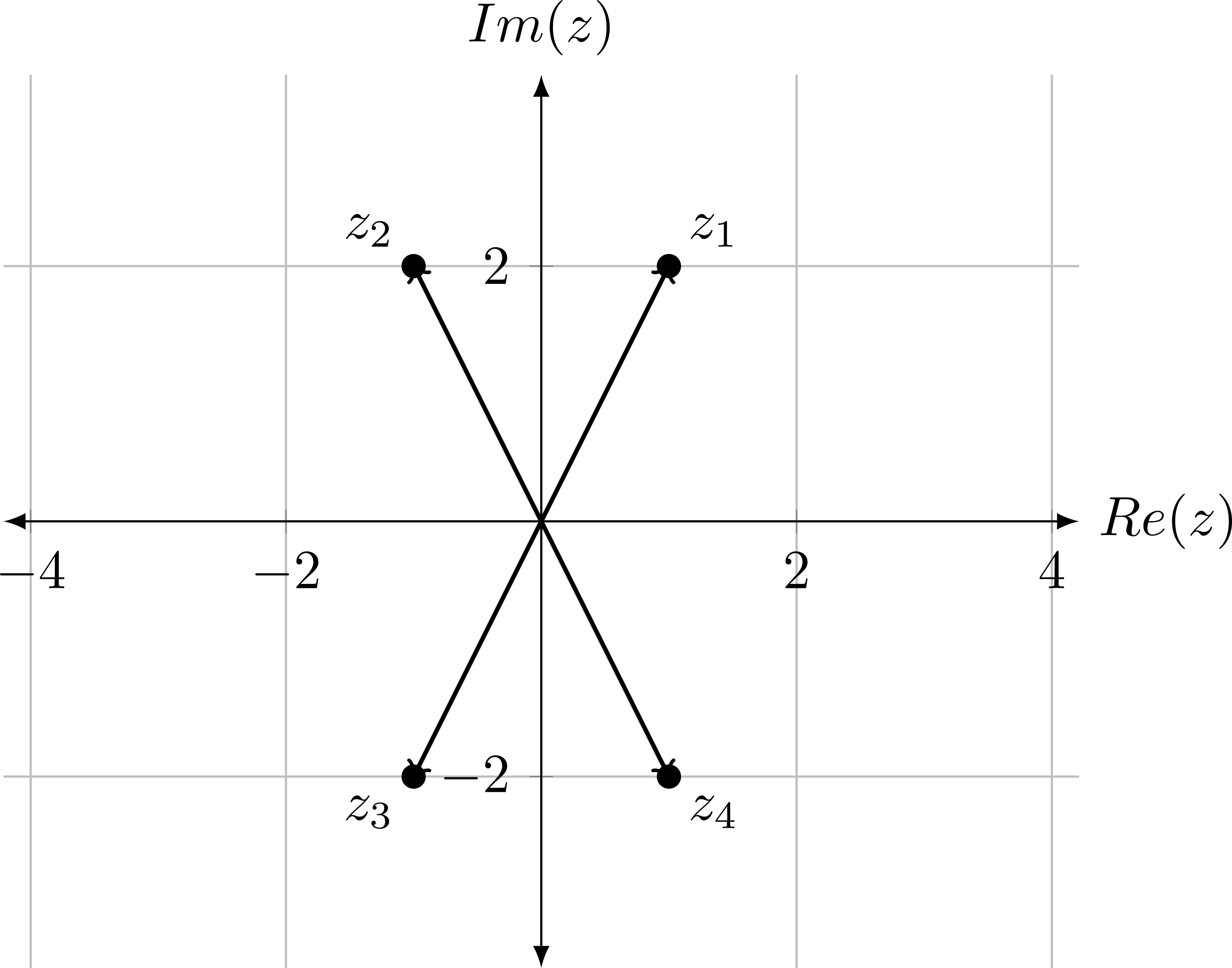
For a complex number \(z = a + jb\) , the magnitude of \(z\) is denoted by \(|z|\) . It represents the distance of a complex number from the origin. Using simple trigonometry: \[\begin{aligned} |z| &= \sqrt{Re(z)^2+Im(z)^2}\\ &= \sqrt{a^2+b^2} \end{aligned}\] Conjugate of a complex number \(z = a+jb\) is denoted by \(z^*\) . It obtained by replacing \(j\) by \(-j\) in the expression of \(z\) .

Forms of a Complex Number #

Complex numbers can be represented in 3 forms:

1. Rectangular Form (also known as Cartesian form)
2. Exponential Form
3. Polar Form

Rectangular Form #

A complex number is expressed in Rectangular (Cartesian) form as \[\begin{aligned} z = a + jb \quad\text{where}\thickspace &a = Re(z)\\ &b = Im(z) \end{aligned}\]

Exponential Form #

Consider the following complex number mapped in the complex plane: 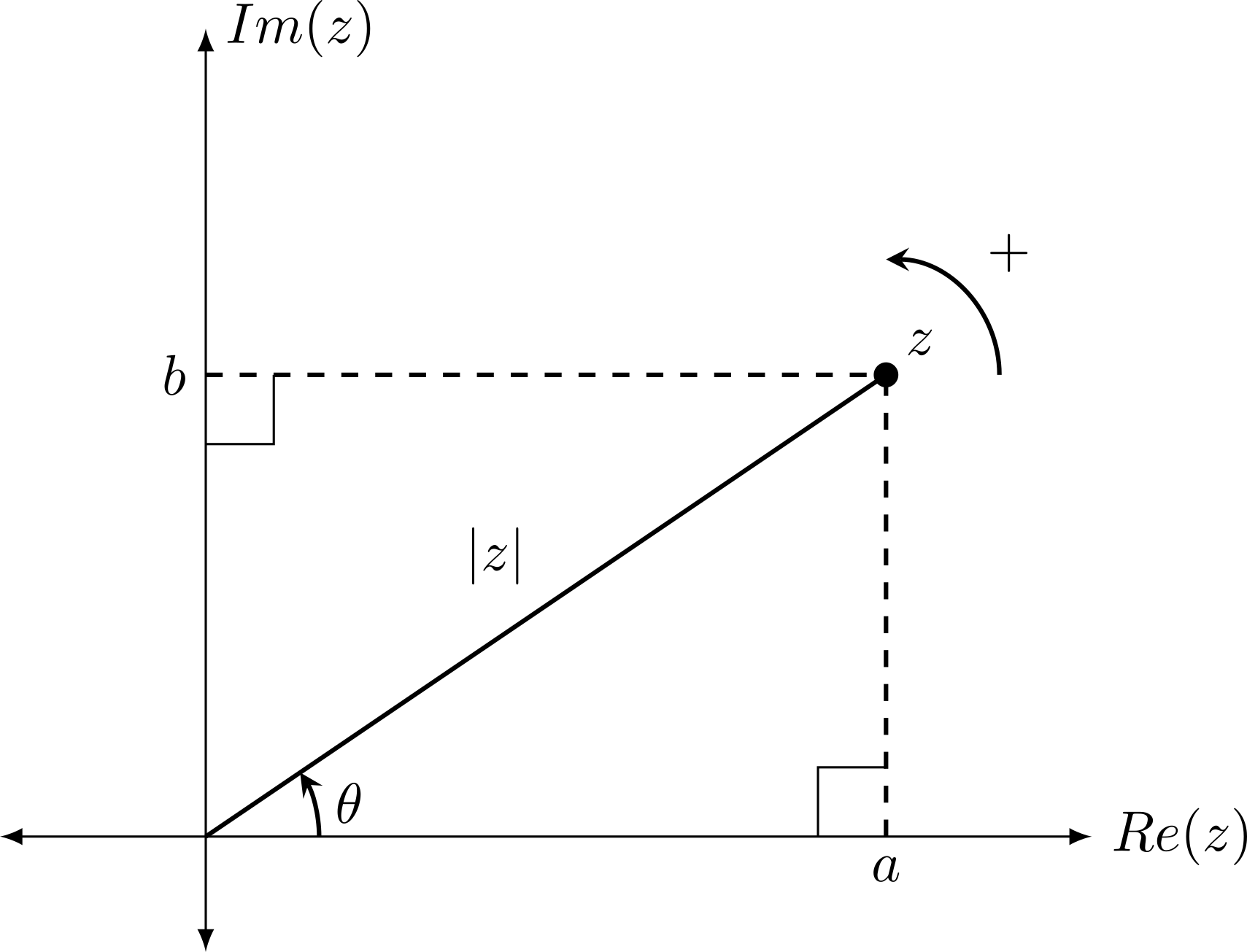Then the following applies: \[a = |z|\cos{\theta}\\ b = |z|\sin{\theta}\] \[\dfrac{b}{a} = \dfrac{|z|\sin{\theta}}{|z|\cos{\theta}} = \tan{\theta} = \dfrac{Im(z)}{Re(z)}\\\] \[\rArr \theta = \arctan{\Big\lparen \dfrac{b}{a} \Big\rparen} = \arctan{\Big( \dfrac{Im(z)}{Re(z)}\Big)}\] Thus, \[\begin{aligned} z &= a + jb\\ & = |z|\cos{\theta} + j|z|\sin{\theta}\\ & = |z|(\cos{\theta} + j\sin{\theta}) \end{aligned}\] From here, we can introduce a new, and famous, formula.
Euler’s Formula: \[\Large e^{j\theta}=\cos{\theta}+j\sin{\theta}\]

Now, using Euler’s formula: \[\begin{aligned} z &= |z|(\cos{\theta}+j\sin{\theta})\\ &= |z|e^{j\theta} \end{aligned}\] This is known as the exponential form.

Note on the angle of a complex number #

Consider the formula we derived earlier for the angle \(\theta\) : \[\theta = \arctan{\Big( \dfrac{Im(z)}{Re(z)}\Big)}\] There is a problem. Inverse tangent only has a valid range of \((-\frac{\pi}{2},\frac{\pi}{2})\) This unfortunately means that this formula does not work properly for complex numbers in the second and third quadrant of the complex plane, when its real component is negative.

This makes sense. When considering the fraction \(Im(z)/Re(z)\) , the resulting ratio is indifferent to whether or not the imaginary value or real value is negative. In other words, these resulting ratios are equivalent: \[\dfrac{-Im(z)}{Re(z)}=\dfrac{Im(z)}{-Re(z)}\] \[\dfrac{-Im(z)}{-Re(z)}=\dfrac{Im(z)}{Re(z)}\]

This means that the formula for our angle in its current form is inaccurate for complex numbers with a negative real component. To remedy this, it is helpful to picture a complex number in the complex plane when its real and imaginary components are known.

• When the real component is less than 0, i.e. negative, the complex number is either in the second or third quadrants.
• If the imaginary component is less than 0, i.e. negative, the complex number is either in the third or fourth quadrants.

Using this:

• If \((Re(z) < 0) \land (Im(z) > 0) \) , then \(\frac{\pi}{2} < \theta < \pi\)
• If \((Re(z) < 0) \land (Im(z) < 0) \) , then \(-\pi < \theta < -\frac{\pi}{2} \)

From here, we can now derive a better formula for the angle of a complex number: \[\theta = \begin{cases} \arctan{\Big( \dfrac{Im(z)}{Re(z)}\Big)} &\text{if } Re(z) > 0 \\ \arctan{\Big( \dfrac{Im(z)}{Re(z)}\Big)} + \pi &\text{if } Re(z) < 0 \land Im(z) > 0\\ \arctan{\Big( \dfrac{Im(z)}{Re(z)}\Big)} - \pi &\text{if } Re(z) < 0 \land Im(z) < 0 \end{cases}\]

If you are slightly more mathematically savvy, you might realize that this formula can technically be combined into the more compact piecewise formula: \[\theta = \begin{cases} \arctan{\Big( \dfrac{Im(z)}{Re(z)}\Big)} &\text{if } Re(z) > 0 \\ \arctan{\Big( \dfrac{Im(z)}{Re(z)}\Big)} \plusmn \pi &\text{if } Re(z) < 0 \end{cases}\]

Exponential Form Example #

Express the following complex numbers in exponential form:

Polar Form #

A complex number is expressed in polar form as: \[z = |z| \angle \theta\]

Complex Number Algebra #

Let \(z_1 = a + jb\) and \(z_2 = c + jd\)

• Addition: Calculate \(z_a = z_1 + z_2\) \[\begin{aligned} &= (a + jb)+(c + jd)\\ &= (a+c) + j(b + d) \end{aligned}\]
• Subtraction: Calculate \(z_s = z_1 - z_2\) \[\begin{aligned} &= (a + jb)-(c + jd)\\ &= (a-c) + j(b - d) \end{aligned}\]
• Multiplication: Calculate \(z_m = z_1 * z_2\) \[\begin{aligned} &= (a + jb)(c + jd)\\ &= ac + j(ad) + j(bc) + jb(jd)\\ &= ac + j(ad + bc) - bd \end{aligned}\]
• Division: Calculate \(z_d = z_1 / z_2\) \[\begin{aligned} &= \frac{a+jb}{c+jd}\\ &= \frac{(a+jb)(c-jd)}{(c+jd)(c-jd)}\\ &= \frac{ac-jad+jbc-j^2bd}{c^2-jcd+jcd-j^2d^2}\\ &= \frac{ac+bd+j(bc-ad)}{c^2+d^2}\\ &= \frac{ac+bd}{c^2+d^2} + j\frac{bc-ad}{c^2+d^2} \end{aligned}\]

Multiplying by its Conjugate #

In the division example, we multiply both parts of the fraction by the conjugate of the denominator, or \((z_2)^{*}\) .

This allows us to create a difference of squares, which removes the imaginary part of the denominator, allowing us to simplify our fraction, and eventually split it into the form \(a+jb\) .

However, some of those more keen-eyed may have noticed something familiar about the denominator when multiplying a complex number by its conjugate. Let’s explore it a bit further:

Let us define a complex number: \(z = a + jb\) .

Therefore, \[z^{*} = a - jb\]

Now let us calculate \(z \times z^{*}\) as we described earlier: \[\begin{aligned} z \times z^{*} &= (a+jb)(a-jb)\\ &= a(a) + a(-jb) + jb(a) + jb(-jb)\\ &= a^2 - jab + jab - j^2b^2\\ &= a^2 + b^2 \end{aligned}\]

This looks suspiciously similar to another equation we saw earlier: the magnitude of a complex number, \(|z|\) . In fact, if we square \(|z|\) , we get the exact same value: \[\begin{aligned} |z|^2 &= (\sqrt{a^2+b^2})^2\\ &= a^2 + b^2 \end{aligned}\]

Essentially, this means we can conclude: \[\begin{aligned} zz^{*} \equiv |z|^2 = a^2 + b^2 \end{aligned}\]

Euler’s Formula #

Earlier, we introduced Euler’s formula: \[e^{j\theta} = \cos{\theta}+j\sin{\theta}\]

Now, we can build upon this formula. Using trigonometric identities, namely the fact that \(\cos{(-\theta)} = \cos{\theta}\) and \(\sin{(-\theta)} = -\sin{\theta}\) , it holds that the following is true: \[e^{-j\theta} = \cos{\theta}-j\sin{\theta}\]

Using these two, we can now further manipulate Euler’s formula to prove the following: \[\begin{aligned} e^{j\theta} + e^{-j\theta} &= (\cos{\theta}+j\sin{\theta}) + (\cos{\theta}-j\sin{\theta})\\ &= 2\cos{\theta} \end{aligned}\] \[\begin{aligned} e^{j\theta} - e^{-j\theta} &= (\cos{\theta}+j\sin{\theta}) - (\cos{\theta}-j\sin{\theta})\\ &= 2j\sin{\theta} \end{aligned}\] Therefore, \[\frac{e^{j\theta} + e^{-j\theta}}{2} = \cos{\theta}\] \[\frac{e^{j\theta} - e^{-j\theta}}{j2} = \sin{\theta}\]

Simplifying Trigonometry #

We can use Euler’s formula to simplify complex trigonometric functions. Consider the following example: \[\begin{aligned} \cos^2\!\theta &= \Big(\frac{e^{j\theta} + e^{-j\theta}}{2}\Big)^2\\ &=\frac{1}{4}(e^{j\theta} + e^{-j\theta})^2 \end{aligned}\] We can use Pascal’s Triangle to quickly simplify the binomial on the right side. \[\begin{array}{c|c c} 0 & 1\\ 1 & 1 & 1\\ 2 & 1 & 2 & 1 \\ 3 & 1 & 3 & 3 & 1 \\ 4 & 1 & 4 & 6 & 4 & 1\\ 5 & 1 & 5 & 10 & 10 & 5 & 1 \end{array}\] We then get the following: \[\rArr \frac{1}{4}\Big[ (e^{j\theta})^2(e^{-j\theta})^0 + 2(e^{j\theta})^1(e^{-j\theta})^1 + (e^{j\theta})^0(e^{-j\theta})^2 \Big]\\ \begin{aligned} &= \frac{1}{4}\Big[ (e^{j2\theta})(1) + 2(e^{j\theta})(e^{-j\theta}) + (1)(e^{-j2\theta}) \Big]\\ &= \frac{1}{4}\Big[ e^{j2\theta} + 2 + e^{-j2\theta} \Big]\\ &= \frac{2}{4} + \frac{e^{j2\theta} + e^{-j2\theta}}{4}\\ &= \frac{1}{2} + \frac{2\cos{2\theta}}{4}\\ &= \frac{1}{2} + \frac{\cos{2\theta}}{2} \end{aligned}\]

Note here that we have actually derived the half-angle identity for cosine, which states: \[\cos{\frac{\theta}{2}} = \plusmn\sqrt{ \frac{1+\cos{\theta}}{2} }\\ \rArr (\cos{\frac{\theta}{2}})^2 = \frac{1+\cos{\theta}}{2}\]

Here’s a more complicated example: